Fork me on GitHub
Previous
Faces recognitio... Faces recognition example using eigenfaces and SVMs
 
Up
Examples Examples

This documentation is for scikit-learn version 0.18.dev0 — Other versions

If you use the software, please consider citing scikit-learn.

Model Complexity InfluenceΒΆ

Demonstrate how model complexity influences both prediction accuracy and computational performance.

The dataset is the Boston Housing dataset (resp. 20 Newsgroups) for regression (resp. classification).

For each class of models we make the model complexity vary through the choice of relevant model parameters and measure the influence on both computational performance (latency) and predictive power (MSE or Hamming Loss).

  • ../../_images/plot_model_complexity_influence_001.png
  • ../../_images/plot_model_complexity_influence_002.png
  • ../../_images/plot_model_complexity_influence_003.png

Script output:

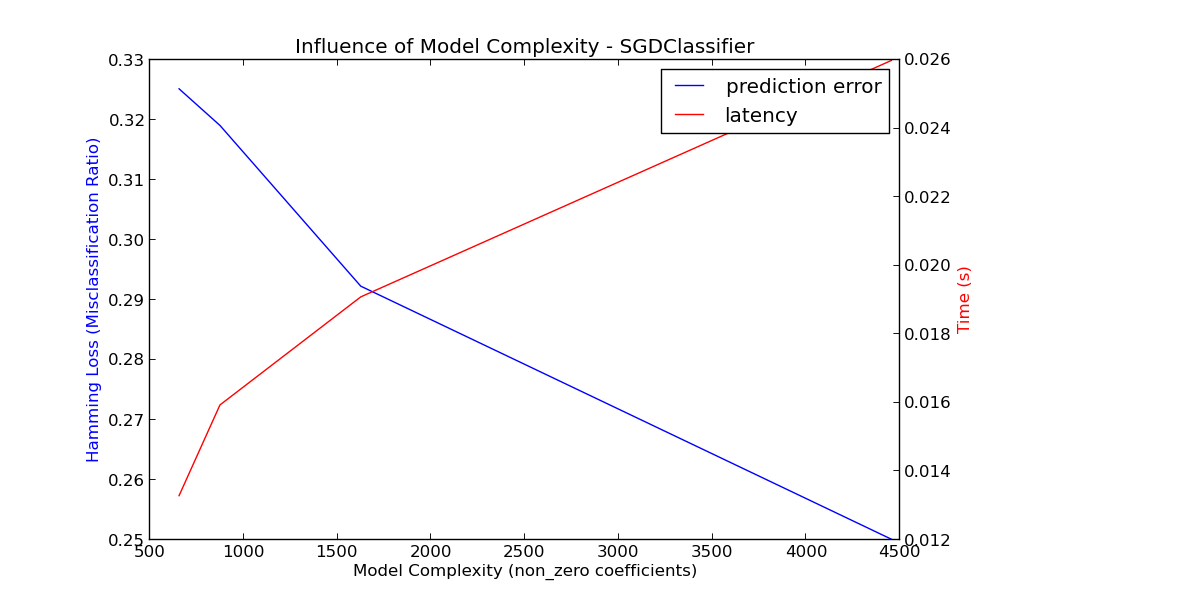
Benchmarking SGDClassifier(alpha=0.001, average=False, class_weight=None, epsilon=0.1,
       eta0=0.0, fit_intercept=True, l1_ratio=0.25,
       learning_rate='optimal', loss='modified_huber', n_iter=5, n_jobs=1,
       penalty='elasticnet', power_t=0.5, random_state=None, shuffle=True,
       verbose=0, warm_start=False)
Complexity: 4454 | Hamming Loss (Misclassification Ratio): 0.2501 | Pred. Time: 0.025987s

Benchmarking SGDClassifier(alpha=0.001, average=False, class_weight=None, epsilon=0.1,
       eta0=0.0, fit_intercept=True, l1_ratio=0.5, learning_rate='optimal',
       loss='modified_huber', n_iter=5, n_jobs=1, penalty='elasticnet',
       power_t=0.5, random_state=None, shuffle=True, verbose=0,
       warm_start=False)
Complexity: 1624 | Hamming Loss (Misclassification Ratio): 0.2923 | Pred. Time: 0.019091s

Benchmarking SGDClassifier(alpha=0.001, average=False, class_weight=None, epsilon=0.1,
       eta0=0.0, fit_intercept=True, l1_ratio=0.75,
       learning_rate='optimal', loss='modified_huber', n_iter=5, n_jobs=1,
       penalty='elasticnet', power_t=0.5, random_state=None, shuffle=True,
       verbose=0, warm_start=False)
Complexity: 873 | Hamming Loss (Misclassification Ratio): 0.3191 | Pred. Time: 0.015938s

Benchmarking SGDClassifier(alpha=0.001, average=False, class_weight=None, epsilon=0.1,
       eta0=0.0, fit_intercept=True, l1_ratio=0.9, learning_rate='optimal',
       loss='modified_huber', n_iter=5, n_jobs=1, penalty='elasticnet',
       power_t=0.5, random_state=None, shuffle=True, verbose=0,
       warm_start=False)
Complexity: 655 | Hamming Loss (Misclassification Ratio): 0.3252 | Pred. Time: 0.013293s

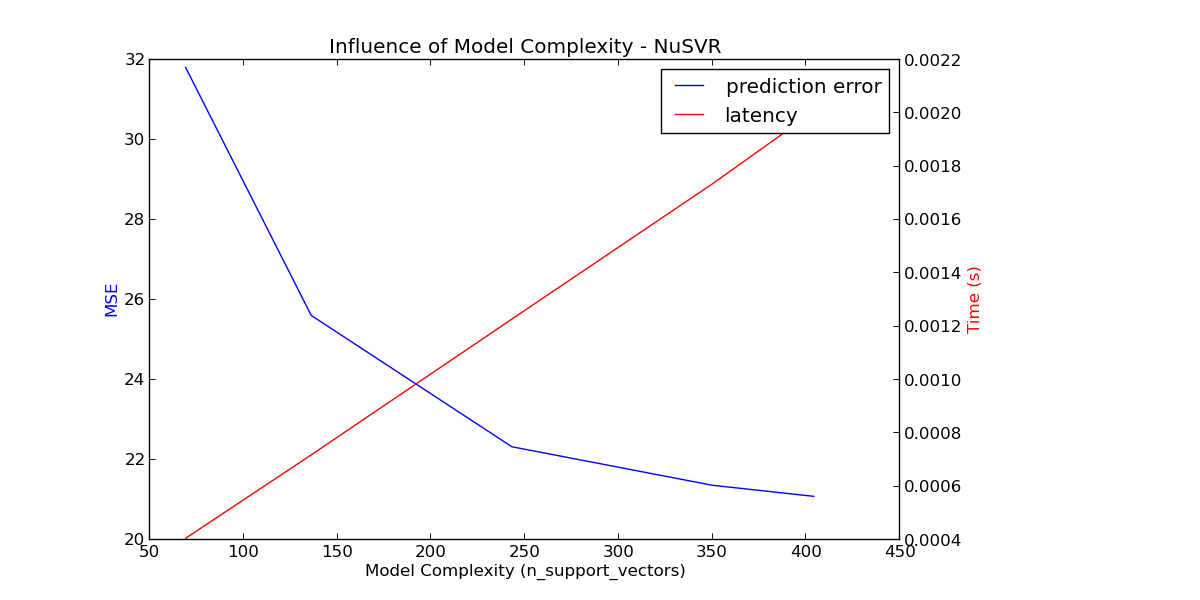
Benchmarking NuSVR(C=1000.0, cache_size=200, coef0=0.0, degree=3, gamma=3.0517578125e-05,
   kernel='rbf', max_iter=-1, nu=0.1, shrinking=True, tol=0.001,
   verbose=False)
Complexity: 69 | MSE: 31.8133 | Pred. Time: 0.000406s

Benchmarking NuSVR(C=1000.0, cache_size=200, coef0=0.0, degree=3, gamma=3.0517578125e-05,
   kernel='rbf', max_iter=-1, nu=0.25, shrinking=True, tol=0.001,
   verbose=False)
Complexity: 136 | MSE: 25.6140 | Pred. Time: 0.000719s

Benchmarking NuSVR(C=1000.0, cache_size=200, coef0=0.0, degree=3, gamma=3.0517578125e-05,
   kernel='rbf', max_iter=-1, nu=0.5, shrinking=True, tol=0.001,
   verbose=False)
Complexity: 243 | MSE: 22.3315 | Pred. Time: 0.001228s

Benchmarking NuSVR(C=1000.0, cache_size=200, coef0=0.0, degree=3, gamma=3.0517578125e-05,
   kernel='rbf', max_iter=-1, nu=0.75, shrinking=True, tol=0.001,
   verbose=False)
Complexity: 350 | MSE: 21.3679 | Pred. Time: 0.001736s

Benchmarking NuSVR(C=1000.0, cache_size=200, coef0=0.0, degree=3, gamma=3.0517578125e-05,
   kernel='rbf', max_iter=-1, nu=0.9, shrinking=True, tol=0.001,
   verbose=False)
Complexity: 404 | MSE: 21.0915 | Pred. Time: 0.002007s

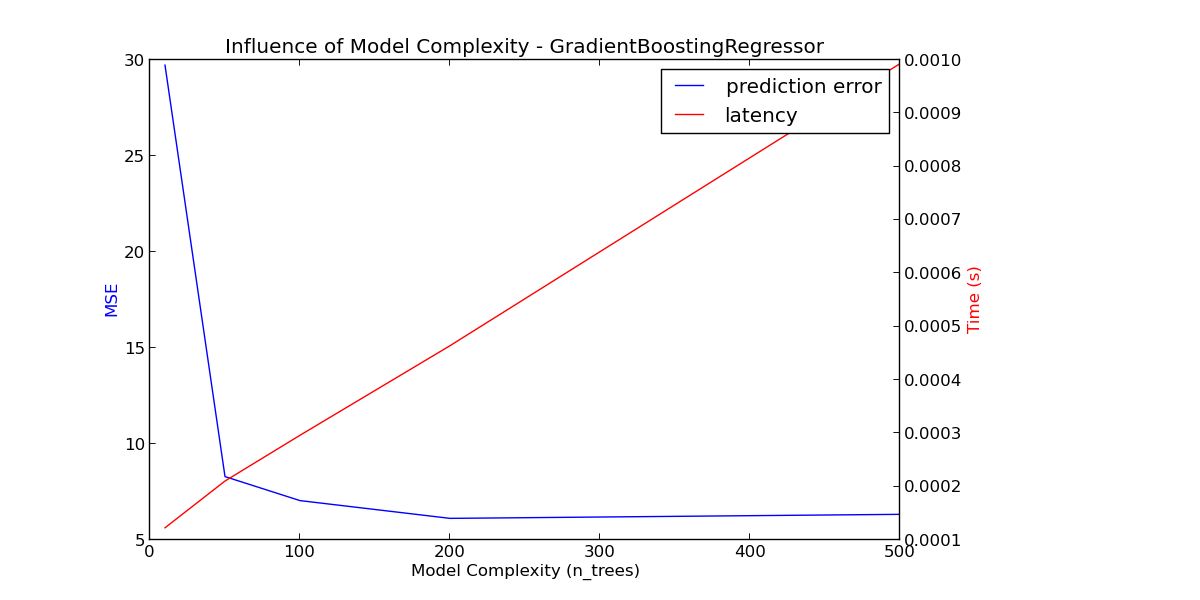
Benchmarking GradientBoostingRegressor(alpha=0.9, init=None, learning_rate=0.1, loss='ls',
             max_depth=3, max_features=None, max_leaf_nodes=None,
             min_samples_leaf=1, min_samples_split=2,
             min_weight_fraction_leaf=0.0, n_estimators=10, presort='auto',
             random_state=None, subsample=1.0, verbose=0, warm_start=False)
Complexity: 10 | MSE: 29.7323 | Pred. Time: 0.000123s

Benchmarking GradientBoostingRegressor(alpha=0.9, init=None, learning_rate=0.1, loss='ls',
             max_depth=3, max_features=None, max_leaf_nodes=None,
             min_samples_leaf=1, min_samples_split=2,
             min_weight_fraction_leaf=0.0, n_estimators=50, presort='auto',
             random_state=None, subsample=1.0, verbose=0, warm_start=False)
Complexity: 50 | MSE: 8.3021 | Pred. Time: 0.000211s

Benchmarking GradientBoostingRegressor(alpha=0.9, init=None, learning_rate=0.1, loss='ls',
             max_depth=3, max_features=None, max_leaf_nodes=None,
             min_samples_leaf=1, min_samples_split=2,
             min_weight_fraction_leaf=0.0, n_estimators=100,
             presort='auto', random_state=None, subsample=1.0, verbose=0,
             warm_start=False)
Complexity: 100 | MSE: 7.0518 | Pred. Time: 0.000296s

Benchmarking GradientBoostingRegressor(alpha=0.9, init=None, learning_rate=0.1, loss='ls',
             max_depth=3, max_features=None, max_leaf_nodes=None,
             min_samples_leaf=1, min_samples_split=2,
             min_weight_fraction_leaf=0.0, n_estimators=200,
             presort='auto', random_state=None, subsample=1.0, verbose=0,
             warm_start=False)
Complexity: 200 | MSE: 6.1267 | Pred. Time: 0.000464s

Benchmarking GradientBoostingRegressor(alpha=0.9, init=None, learning_rate=0.1, loss='ls',
             max_depth=3, max_features=None, max_leaf_nodes=None,
             min_samples_leaf=1, min_samples_split=2,
             min_weight_fraction_leaf=0.0, n_estimators=500,
             presort='auto', random_state=None, subsample=1.0, verbose=0,
             warm_start=False)
Complexity: 500 | MSE: 6.3365 | Pred. Time: 0.000993s

Python source code: plot_model_complexity_influence.py

print(__doc__)

# Author: Eustache Diemert <eustache@diemert.fr>
# License: BSD 3 clause

import time
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.parasite_axes import host_subplot
from mpl_toolkits.axisartist.axislines import Axes
from scipy.sparse.csr import csr_matrix

from sklearn import datasets
from sklearn.utils import shuffle
from sklearn.metrics import mean_squared_error
from sklearn.svm.classes import NuSVR
from sklearn.ensemble.gradient_boosting import GradientBoostingRegressor
from sklearn.linear_model.stochastic_gradient import SGDClassifier
from sklearn.metrics import hamming_loss

###############################################################################
# Routines


# initialize random generator
np.random.seed(0)


def generate_data(case, sparse=False):
    """Generate regression/classification data."""
    bunch = None
    if case == 'regression':
        bunch = datasets.load_boston()
    elif case == 'classification':
        bunch = datasets.fetch_20newsgroups_vectorized(subset='all')
    X, y = shuffle(bunch.data, bunch.target)
    offset = int(X.shape[0] * 0.8)
    X_train, y_train = X[:offset], y[:offset]
    X_test, y_test = X[offset:], y[offset:]
    if sparse:
        X_train = csr_matrix(X_train)
        X_test = csr_matrix(X_test)
    else:
        X_train = np.array(X_train)
        X_test = np.array(X_test)
    y_test = np.array(y_test)
    y_train = np.array(y_train)
    data = {'X_train': X_train, 'X_test': X_test, 'y_train': y_train,
            'y_test': y_test}
    return data


def benchmark_influence(conf):
    """
    Benchmark influence of :changing_param: on both MSE and latency.
    """
    prediction_times = []
    prediction_powers = []
    complexities = []
    for param_value in conf['changing_param_values']:
        conf['tuned_params'][conf['changing_param']] = param_value
        estimator = conf['estimator'](**conf['tuned_params'])
        print("Benchmarking %s" % estimator)
        estimator.fit(conf['data']['X_train'], conf['data']['y_train'])
        conf['postfit_hook'](estimator)
        complexity = conf['complexity_computer'](estimator)
        complexities.append(complexity)
        start_time = time.time()
        for _ in range(conf['n_samples']):
            y_pred = estimator.predict(conf['data']['X_test'])
        elapsed_time = (time.time() - start_time) / float(conf['n_samples'])
        prediction_times.append(elapsed_time)
        pred_score = conf['prediction_performance_computer'](
            conf['data']['y_test'], y_pred)
        prediction_powers.append(pred_score)
        print("Complexity: %d | %s: %.4f | Pred. Time: %fs\n" % (
            complexity, conf['prediction_performance_label'], pred_score,
            elapsed_time))
    return prediction_powers, prediction_times, complexities


def plot_influence(conf, mse_values, prediction_times, complexities):
    """
    Plot influence of model complexity on both accuracy and latency.
    """
    plt.figure(figsize=(12, 6))
    host = host_subplot(111, axes_class=Axes)
    plt.subplots_adjust(right=0.75)
    par1 = host.twinx()
    host.set_xlabel('Model Complexity (%s)' % conf['complexity_label'])
    y1_label = conf['prediction_performance_label']
    y2_label = "Time (s)"
    host.set_ylabel(y1_label)
    par1.set_ylabel(y2_label)
    p1, = host.plot(complexities, mse_values, 'b-', label="prediction error")
    p2, = par1.plot(complexities, prediction_times, 'r-',
                    label="latency")
    host.legend(loc='upper right')
    host.axis["left"].label.set_color(p1.get_color())
    par1.axis["right"].label.set_color(p2.get_color())
    plt.title('Influence of Model Complexity - %s' % conf['estimator'].__name__)
    plt.show()


def _count_nonzero_coefficients(estimator):
    a = estimator.coef_.toarray()
    return np.count_nonzero(a)

###############################################################################
# main code
regression_data = generate_data('regression')
classification_data = generate_data('classification', sparse=True)
configurations = [
    {'estimator': SGDClassifier,
     'tuned_params': {'penalty': 'elasticnet', 'alpha': 0.001, 'loss':
                      'modified_huber', 'fit_intercept': True},
     'changing_param': 'l1_ratio',
     'changing_param_values': [0.25, 0.5, 0.75, 0.9],
     'complexity_label': 'non_zero coefficients',
     'complexity_computer': _count_nonzero_coefficients,
     'prediction_performance_computer': hamming_loss,
     'prediction_performance_label': 'Hamming Loss (Misclassification Ratio)',
     'postfit_hook': lambda x: x.sparsify(),
     'data': classification_data,
     'n_samples': 30},
    {'estimator': NuSVR,
     'tuned_params': {'C': 1e3, 'gamma': 2 ** -15},
     'changing_param': 'nu',
     'changing_param_values': [0.1, 0.25, 0.5, 0.75, 0.9],
     'complexity_label': 'n_support_vectors',
     'complexity_computer': lambda x: len(x.support_vectors_),
     'data': regression_data,
     'postfit_hook': lambda x: x,
     'prediction_performance_computer': mean_squared_error,
     'prediction_performance_label': 'MSE',
     'n_samples': 30},
    {'estimator': GradientBoostingRegressor,
     'tuned_params': {'loss': 'ls'},
     'changing_param': 'n_estimators',
     'changing_param_values': [10, 50, 100, 200, 500],
     'complexity_label': 'n_trees',
     'complexity_computer': lambda x: x.n_estimators,
     'data': regression_data,
     'postfit_hook': lambda x: x,
     'prediction_performance_computer': mean_squared_error,
     'prediction_performance_label': 'MSE',
     'n_samples': 30},
]
for conf in configurations:
    prediction_performances, prediction_times, complexities = \
        benchmark_influence(conf)
    plot_influence(conf, prediction_performances, prediction_times,
                   complexities)

Total running time of the example: 60.29 seconds ( 1 minutes 0.29 seconds)

© 2010 - 2015, scikit-learn developers (BSD License). Show this page source
Previous