sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis¶
- class sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis(priors=None, reg_param=0.0, store_covariances=False, tol=0.0001)[source]¶
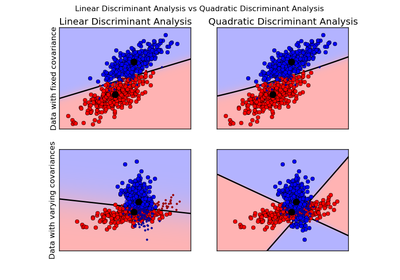
Quadratic Discriminant Analysis
A classifier with a quadratic decision boundary, generated by fitting class conditional densities to the data and using Bayes’ rule.
The model fits a Gaussian density to each class.
New in version 0.17: QuadraticDiscriminantAnalysis
Changed in version 0.17: Deprecated qda.QDA have been moved to QuadraticDiscriminantAnalysis.
Parameters: priors : array, optional, shape = [n_classes]
Priors on classes
reg_param : float, optional
Regularizes the covariance estimate as (1-reg_param)*Sigma + reg_param*np.eye(n_features)
Attributes: covariances_ : list of array-like, shape = [n_features, n_features]
Covariance matrices of each class.
means_ : array-like, shape = [n_classes, n_features]
Class means.
priors_ : array-like, shape = [n_classes]
Class priors (sum to 1).
rotations_ : list of arrays
For each class k an array of shape [n_features, n_k], with n_k = min(n_features, number of elements in class k) It is the rotation of the Gaussian distribution, i.e. its principal axis.
scalings_ : list of arrays
For each class k an array of shape [n_k]. It contains the scaling of the Gaussian distributions along its principal axes, i.e. the variance in the rotated coordinate system.
store_covariances : boolean
If True the covariance matrices are computed and stored in the self.covariances_ attribute.
New in version 0.17.
tol : float, optional, default 1.0e-4
Threshold used for rank estimation.
New in version 0.17.
See also
- sklearn.discriminant_analysis.LinearDiscriminantAnalysis
- Linear Discriminant Analysis
Examples
>>> from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis >>> import numpy as np >>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]]) >>> y = np.array([1, 1, 1, 2, 2, 2]) >>> clf = QuadraticDiscriminantAnalysis() >>> clf.fit(X, y) ... QuadraticDiscriminantAnalysis(priors=None, reg_param=0.0, store_covariances=False, tol=0.0001) >>> print(clf.predict([[-0.8, -1]])) [1]
Methods
decision_function(X) Apply decision function to an array of samples. fit(X, y[, store_covariances, tol]) Fit the model according to the given training data and parameters. get_params([deep]) Get parameters for this estimator. predict(X) Perform classification on an array of test vectors X. predict_log_proba(X) Return posterior probabilities of classification. predict_proba(X) Return posterior probabilities of classification. score(X, y[, sample_weight]) Returns the mean accuracy on the given test data and labels. set_params(**params) Set the parameters of this estimator. - decision_function(X)[source]¶
Apply decision function to an array of samples.
Parameters: X : array-like, shape = [n_samples, n_features]
Array of samples (test vectors).
Returns: C : array, shape = [n_samples, n_classes] or [n_samples,]
Decision function values related to each class, per sample. In the two-class case, the shape is [n_samples,], giving the log likelihood ratio of the positive class.
- fit(X, y, store_covariances=None, tol=None)[source]¶
Fit the model according to the given training data and parameters.
Changed in version 0.17: Deprecated store_covariance have been moved to main constructor.
Changed in version 0.17: Deprecated tol have been moved to main constructor.
Parameters: X : array-like, shape = [n_samples, n_features]
Training vector, where n_samples in the number of samples and n_features is the number of features.
y : array, shape = [n_samples]
Target values (integers)
- get_params(deep=True)[source]¶
Get parameters for this estimator.
Parameters: deep: boolean, optional :
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: params : mapping of string to any
Parameter names mapped to their values.
- predict(X)[source]¶
Perform classification on an array of test vectors X.
The predicted class C for each sample in X is returned.
Parameters: X : array-like, shape = [n_samples, n_features] Returns: C : array, shape = [n_samples]
- predict_log_proba(X)[source]¶
Return posterior probabilities of classification.
Parameters: X : array-like, shape = [n_samples, n_features]
Array of samples/test vectors.
Returns: C : array, shape = [n_samples, n_classes]
Posterior log-probabilities of classification per class.
- predict_proba(X)[source]¶
Return posterior probabilities of classification.
Parameters: X : array-like, shape = [n_samples, n_features]
Array of samples/test vectors.
Returns: C : array, shape = [n_samples, n_classes]
Posterior probabilities of classification per class.
- score(X, y, sample_weight=None)[source]¶
Returns the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters: X : array-like, shape = (n_samples, n_features)
Test samples.
y : array-like, shape = (n_samples) or (n_samples, n_outputs)
True labels for X.
sample_weight : array-like, shape = [n_samples], optional
Sample weights.
Returns: score : float
Mean accuracy of self.predict(X) wrt. y.
- set_params(**params)[source]¶
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The former have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.
Returns: self :