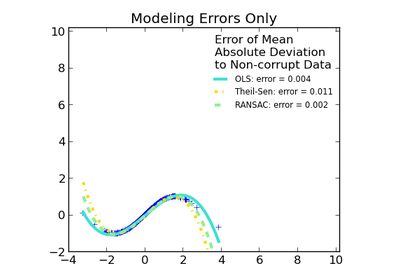
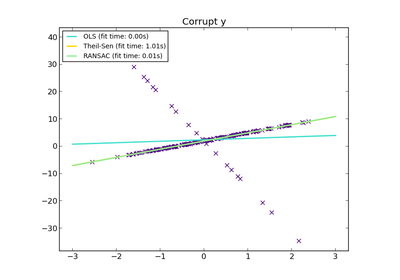
sklearn.linear_model.TheilSenRegressor¶
- class sklearn.linear_model.TheilSenRegressor(fit_intercept=True, copy_X=True, max_subpopulation=10000.0, n_subsamples=None, max_iter=300, tol=0.001, random_state=None, n_jobs=1, verbose=False)[source]¶
Theil-Sen Estimator: robust multivariate regression model.
The algorithm calculates least square solutions on subsets with size n_subsamples of the samples in X. Any value of n_subsamples between the number of features and samples leads to an estimator with a compromise between robustness and efficiency. Since the number of least square solutions is “n_samples choose n_subsamples”, it can be extremely large and can therefore be limited with max_subpopulation. If this limit is reached, the subsets are chosen randomly. In a final step, the spatial median (or L1 median) is calculated of all least square solutions.
Read more in the User Guide.
Parameters: fit_intercept : boolean, optional, default True
Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations.
copy_X : boolean, optional, default True
If True, X will be copied; else, it may be overwritten.
max_subpopulation : int, optional, default 1e4
Instead of computing with a set of cardinality ‘n choose k’, where n is the number of samples and k is the number of subsamples (at least number of features), consider only a stochastic subpopulation of a given maximal size if ‘n choose k’ is larger than max_subpopulation. For other than small problem sizes this parameter will determine memory usage and runtime if n_subsamples is not changed.
n_subsamples : int, optional, default None
Number of samples to calculate the parameters. This is at least the number of features (plus 1 if fit_intercept=True) and the number of samples as a maximum. A lower number leads to a higher breakdown point and a low efficiency while a high number leads to a low breakdown point and a high efficiency. If None, take the minimum number of subsamples leading to maximal robustness. If n_subsamples is set to n_samples, Theil-Sen is identical to least squares.
max_iter : int, optional, default 300
Maximum number of iterations for the calculation of spatial median.
tol : float, optional, default 1.e-3
Tolerance when calculating spatial median.
random_state : RandomState or an int seed, optional, default None
A random number generator instance to define the state of the random permutations generator.
n_jobs : integer, optional, default 1
Number of CPUs to use during the cross validation. If -1, use all the CPUs.
verbose : boolean, optional, default False
Verbose mode when fitting the model.
Attributes: coef_ : array, shape = (n_features)
Coefficients of the regression model (median of distribution).
intercept_ : float
Estimated intercept of regression model.
breakdown_ : float
Approximated breakdown point.
n_iter_ : int
Number of iterations needed for the spatial median.
n_subpopulation_ : int
Number of combinations taken into account from ‘n choose k’, where n is the number of samples and k is the number of subsamples.
References
- Theil-Sen Estimators in a Multiple Linear Regression Model, 2009 Xin Dang, Hanxiang Peng, Xueqin Wang and Heping Zhang http://www.math.iupui.edu/~hpeng/MTSE_0908.pdf
Methods
decision_function(*args, **kwargs) DEPRECATED: and will be removed in 0.19. fit(X, y) Fit linear model. get_params([deep]) Get parameters for this estimator. predict(X) Predict using the linear model score(X, y[, sample_weight]) Returns the coefficient of determination R^2 of the prediction. set_params(**params) Set the parameters of this estimator. - __init__(fit_intercept=True, copy_X=True, max_subpopulation=10000.0, n_subsamples=None, max_iter=300, tol=0.001, random_state=None, n_jobs=1, verbose=False)[source]¶
- decision_function(*args, **kwargs)[source]¶
DEPRECATED: and will be removed in 0.19.
Decision function of the linear model.
Parameters: X : {array-like, sparse matrix}, shape = (n_samples, n_features)
Samples.
Returns: C : array, shape = (n_samples,)
Returns predicted values.
- fit(X, y)[source]¶
Fit linear model.
Parameters: X : numpy array of shape [n_samples, n_features]
Training data
y : numpy array of shape [n_samples]
Target values
Returns: self : returns an instance of self.
- get_params(deep=True)[source]¶
Get parameters for this estimator.
Parameters: deep: boolean, optional :
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns: params : mapping of string to any
Parameter names mapped to their values.
- predict(X)[source]¶
Predict using the linear model
Parameters: X : {array-like, sparse matrix}, shape = (n_samples, n_features)
Samples.
Returns: C : array, shape = (n_samples,)
Returns predicted values.
- score(X, y, sample_weight=None)[source]¶
Returns the coefficient of determination R^2 of the prediction.
The coefficient R^2 is defined as (1 - u/v), where u is the regression sum of squares ((y_true - y_pred) ** 2).sum() and v is the residual sum of squares ((y_true - y_true.mean()) ** 2).sum(). Best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a R^2 score of 0.0.
Parameters: X : array-like, shape = (n_samples, n_features)
Test samples.
y : array-like, shape = (n_samples) or (n_samples, n_outputs)
True values for X.
sample_weight : array-like, shape = [n_samples], optional
Sample weights.
Returns: score : float
R^2 of self.predict(X) wrt. y.
- set_params(**params)[source]¶
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The former have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.
Returns: self :