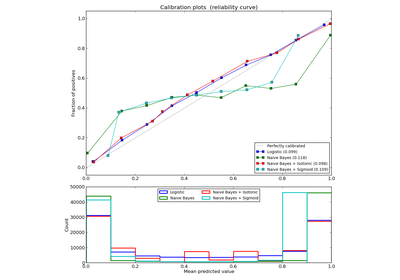
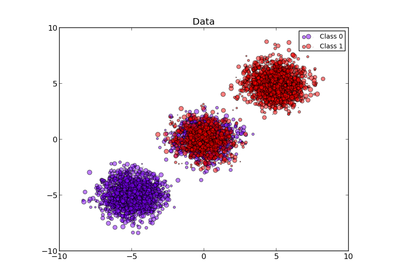
sklearn.metrics.brier_score_loss

sklearn.metrics.brier_score_loss(y_true, y_prob, sample_weight=None, pos_label=None)

Compute the Brier score.

The smaller the Brier score, the better, hence the naming with “loss”.

Across all items in a set N predictions, the Brier score measures the mean squared difference between (1) the predicted probability assigned to the possible outcomes for item i, and (2) the actual outcome. Therefore, the lower the Brier score is for a set of predictions, the better the predictions are calibrated. Note that the Brier score always takes on a value between zero and one, since this is the largest possible difference between a predicted probability (which must be between zero and one) and the actual outcome (which can take on values of only 0 and 1).

The Brier score is appropriate for binary and categorical outcomes that can be structured as true or false, but is inappropriate for ordinal variables which can take on three or more values (this is because the Brier score assumes that all possible outcomes are equivalently “distant” from one another). Which label is considered to be the positive label is controlled via the parameter pos_label, which defaults to 1.

Read more in the User Guide.

Parameters:

y_true : array, shape (n_samples,)

True targets.

y_prob : array, shape (n_samples,)

Probabilities of the positive class.

sample_weight : array-like of shape = [n_samples], optional

Sample weights.

pos_label : int (default: None)

Label of the positive class. If None, the maximum label is used as positive class

Returns:

score : float

Brier score

References

http://en.wikipedia.org/wiki/Brier_score

Examples

>>> import numpy as np
>>> from sklearn.metrics import brier_score_loss
>>> y_true = np.array([0, 1, 1, 0])
>>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"])
>>> y_prob = np.array([0.1, 0.9, 0.8, 0.3])
>>> brier_score_loss(y_true, y_prob)  
0.037...
>>> brier_score_loss(y_true, 1-y_prob, pos_label=0)  
0.037...
>>> brier_score_loss(y_true_categorical, y_prob,                          pos_label="ham")  
0.037...
>>> brier_score_loss(y_true, np.array(y_prob) > 0.5)
0.0

Examples using sklearn.metrics.brier_score_loss

Probability Calibration curves

Probability calibration of classifiers